Collatz Conjecture এর আলাপ
— Number Theory, Mathemetics — 3 min read
১ থেকে ১০ পর্যন্ত একটি সঙ্খ্যা নিন। ৭? আশ্চর্যের কিছু নেই। এটি বৈজ্ঞানিক ভাবে পরীক্ষিত যে ৭ পছন্দ করার হার বেশী। তাহলে ৭ ধরেই এগুই। প্রথমেই খেলার নিয়ম বলে দেই। সঙ্খ্যাটি যদি বিজোর হয় তাহলে তার সাথে ৩ গুন করে ১ যোগ করতে হবে। আর জোড় হলে করতে হবে ২ দিয়ে ভাগ। এভাবে এগুতে থাকতে হবে। কল্পনা করুন তো কত দূর যাওয়া যেতে পারে এভাবে?
আচ্ছা সহজ করে দেই। আমারা যদি আমাদের সূত্রধরে এগুই, তাহল আমরা পাব ৭, ২২, ১১, ৩৪, ১৭, ৫২, ২৬, ১৩, ৪০, ২০, ১০, ৫, ১৬, ৮, ৪, ২, ১। খেয়াল করে দেখুন শেষের সংখ্যাটি ১ যা কি না বিজোড় সংখ্যা। যদি আমরা আমাদের সূত্র মেনে এঁকে ৩ দিয়ে গুণ করে ১ যোগ করি তাহল আমরা পাব ৪। লিস্ট টা যদি আবার খেয়াল করেন তাহলে দেখবেন সেখানে ৪ পূর্ব থেকেই আছে এবং তা পুনরায় ১ এ গিয়ে শেষ হয়েছে। অর্থাৎ এখানে একটি ল্যুপের সৃষ্টি হয়েছে যা কখনোই শেষ হবার নয়।
এবার সংখ্যা গুলোকে যদি আমরা গ্রাফ পেপারে বসাই তাহলে কিছুটা নিচের মত ফলাফল পাব। সুন্দর না?
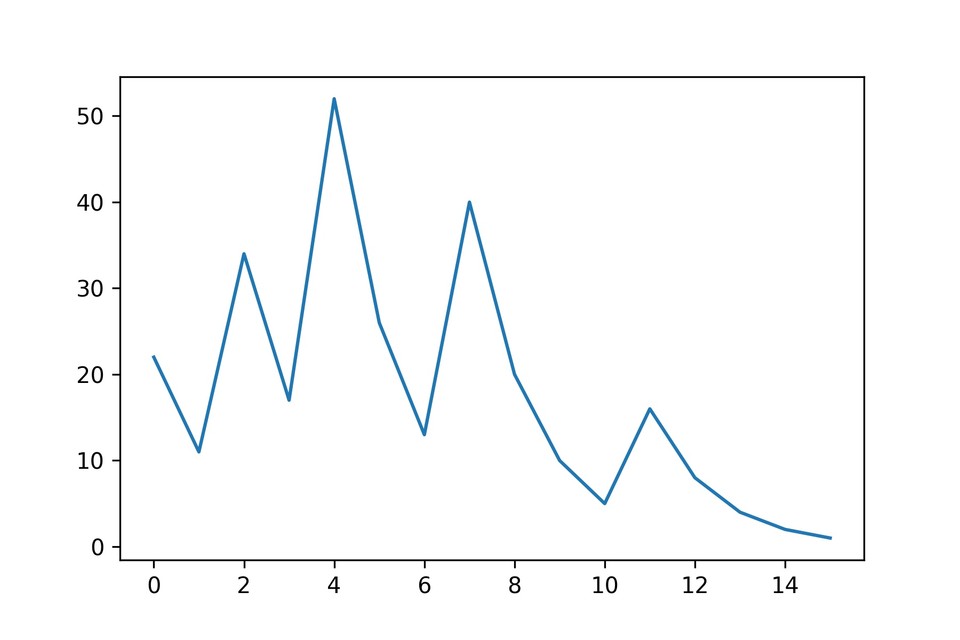
এখন প্রশ্ন হচ্ছে সকল ধ্বন্যাত্মক পূর্ণ সখ্যাই কি ১ এ গিয়ে শেষ হবে? আর যদি হয় তাহলে তার শক্ত প্রমাণ কি? মজার বিষয় হচ্ছে এটি গণিত শাস্ত্রের অমিমাংসিত সমস্যা সমূহের মধ্যে একটি, যেটির সঠিক রূপ আজ অবধি প্রমাণ করা সম্ভব হয়নি। যাকগে এসব কথা, আমরা আবার গ্রাফে ফিরে যাই।
উপরে আমরা দেখলাম শুধু ৭ এর গ্রাফ, অনেকটা পাহাড়ের মত তাই না? চলুন, এবার এই গ্রাফে আরো সঙ্খ্যার জন্য রেখা অঙ্কন করি। এজন্য প্রথমে ৩ থেকে ২৬ পর্যন্ত সঙ্খ্যার উপর আমাদের এল্গোরিদম প্রয়োগ করা যাক।
1from tqdm import tqdm2import timeit3
4start = timeit.timeit()5values = []6for x in tqdm(range(3, 1000)):7 temp = []8 while x > 1:9 if x % 2 != 0:10 x = int((x*3)+1)11 temp.append(x)12 else:13 x = int(x/2)14 temp.append(x)15 values.append(temp)16
17end = timeit.timeit()18print("Time taken - ", end - start)19print(values)20
21# Time taken - 0.0003476999999999924622# [[10, 5, 16, 8, 4, 2, 1], 23# [2, 1], 24# [16, 8, 4, 2, 1], 25# ......26# [7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1], 27# [46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1], 28# ......29# [9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1],30# [58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1],31# ......এখন আমরা প্রাপ্ত ফল গুলোকে (৩ থেকে ২৬ পর্যন্ত) গ্রাফে বসালে নিচের মত ফলাফল পাব।
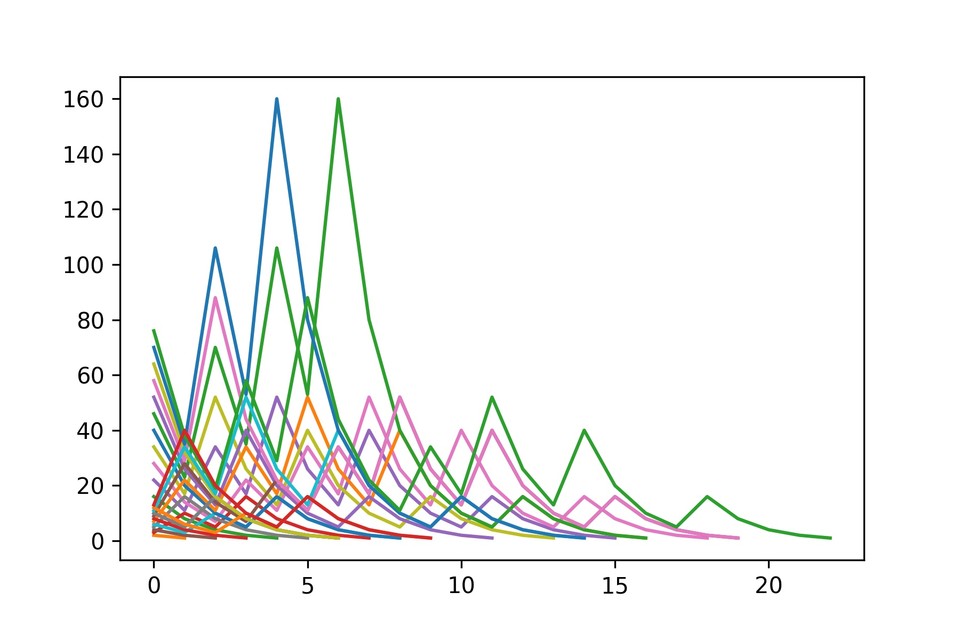
আমাদের গ্রাফ এবার পাহার পুঞ্জের মত হয়ে গেছে তাই না? সুন্দর।
এই এল্গোরিদমে আমরা values নামে একটি লিস্ট ডাটাস্ট্রাকচারের কালেকশন নিয়েছি। এর পর ৩ থেকে ১০০০ পর্যন্ত একটি লুপ নিয়েছি।
প্রতি লুপে একটি temp নামে আরো একটি লিস্ট নিয়ে একটি হোয়ালি লুপ চালিয়ে আমাদের সঙ্খ্যাটিকে সুত্রে ফেলে সব
মান বের করে এতে রেখেছি। ল্যুপ শেষ হলে temp নামের এই লিস্ট টাকে আমাদের মেইন কালেকশন values
এ যোগ করে দিয়েছি। এভাবে প্রতি সঙ্খ্যার জন্য নতুন করে temp নিয়ে আমাদের values লিস্ট কে পূর্ণ করেছি।
এবং সব শেষে আমাদের values লিস্টটাকে প্রিন্ট করে দিয়েছি। আর values ইনিশিয়ালাইজেশন থেকে শুরু করে
ফর লুপ শেষ হওয়া পর্যন্ত ক্যালকুলেশন করতে কত টাইম লেগেছে তা নির্ণয়ের জন্য আমরা timeit()
ফাংশন ব্যবহার করেছি।
বিঃদ্রঃ ক্যালকুলেশন এর সময় কত লাগবে তা কন্সট্যান্ট নয়। এটি মেশিন কনফিগারেশন ও প্রসেসরের লোডের উপর নির্ভরশীল।
কিন্ত এখানে একটি সমস্যা রয়েছে। সেটি যদি খেয়াল করেন তাহলে লক্ষ্য করবেন প্রতিটি সঙ্খ্যার জন্যই কিন্ত ৪ থেকে ১ পর্যন্ত বার বার গণনা করতে হচ্ছে। শুধু তাই নয়, ১৮ এবং ১৯ দুইটি সখ্যার জন্যই কিন্ত ২২ থেকে গণনা করতে হয়েছে (আউটপুট উদাহরণের ৩০ ও ৩১ নম্বর লাইন) । এই অতিরিক্ত গণনাকে আমরা কিভাবে কমাতে পারি?
ঠিক ধরেছেন। আগের গণনা করা মান কে পুনরায় ব্যাবহার করে। এই পদ্ধতিকে বলা হয় মেমোয়াইজেশন। কম্পিউটার সাইন্সের মেমোয়াইজেশন হচ্ছে প্রোগ্রামকে দ্রুত গতিতে চালনা করার পদ্ধতি গুলোর একটি। এই পদ্ধতিতে ব্যায়বহুল ফাংশন কলগুলোকে সেভ করে রাখা হয়। পরবর্তীতে একই গণনার দরকার হলে পুনরায় সেই ফাংশন কল না করে সেভ করে রাখা উত্তর ব্যাবহার করা হয়।
আচ্ছা আমরা মেমোয়াইজেশন কি তা জানলাম, এখন তা ইমপ্লিমেন্ট করব কিভাবে? এই ঝামেলা থেকে আমাদের মুক্তি দেয়ার জন্য স্মারট ল্যাঙ্গুয়েজ ডিজাইনার রা ইতিমধ্যে ডিকশনারি নামে একটি ডাটা স্ট্রাকচার তৈরি করে রেখেছেন। ডিকশনারি ডেটা স্ট্রাকচার কিভাবে কাজ করে তা আর আজকে আলোচোনা করছি না তবে এটুকু বলে রাখা যায় যে ডিকশনারি কন্সট্যান্ট টাইমে ভ্যালু রিটার্ন করে। ধরুন একটি ইংরেজী থেকে বাংলার ডিকশনারিকে আমি জিগ্যেস করলাম যে “House” মানে কি, সে A থেকে দেখা শুরু না করে সরাসরি “House” এর অর্থ চেক করে “বাসা/বাড়ি” রিটার্ন করবে। যাহোক, এবার আমরা ডিকশনারি ব্যাবহার করে মেমোয়াইজেশন ইমপ্লিমেন্ট করে ফেলি!
1from tqdm import tqdm2import timeit3
4start = timeit.timeit()5values = []6memory = {}7for x in tqdm(range(3, 27)):8 temp = []9 p = x10 while x != 1:11 try:12 temp += memory[x][1]13 memory[x][0] = memory[x][0] + 114 break15 except:16 pass17 if x % 2 != 0:18 x = int((x*3)+1)19 temp.append(x)20 else:21 x = int(x/2)22 temp.append(x)23 memory[p] = [1, temp]24 values.append(temp)25end = timeit.timeit()26print("Time taken - ", end - start)27
28# Time Taken - 0.00003729999999998318এবার দ্বিতীয় এল্গোরিদমে আমরা প্রথম এল্গোরিদম কে মডিফাই করেছি। values ইনিশিয়ালাইজেশনের
পাশাপাশি আমরা memory নামে একটি ডিকশনারি ইনিশিয়ালাইজ করেছি। এর পরে হোয়াইল লুপে
আমরা প্রথমে চেক করেছি যে গণনা করার জন্য যে সঙ্খ্যাটি বর্তমানে হাতে রয়েছে সেটি ডিকশনারিতে
আছে কি না, যদি থাকে তবে পুনরায় উত্তর গণনা না করে সেই ভ্যালু কে কপি করে আমাদের temp
লিস্টে এনে যোগ করেছি এবং ল্যুপ শেষ করে দিয়েছি। আর যদি না থাকে তাহলে বরাবরের মত সুত্র
দিয়ে উত্তর বের করেছি। উল্লেখ্য যে ডিকশনারিতে যদি কোন ভ্যালু না থাকে আর সেটি যদি আমরা
এক্সেস করতে চাই তবে পাইথন ইন্ট্রপ্রেটার এক্সেপশন ত্রো করবে। সেজন্য আমরা ডিকশনারি চেকিং এর
কাজটি try…except ব্লকের মাঝে করেছি।
এবার যদি আমরা সময়ের দিকে তাকাই তাহলে দেখতে পাব ৩ থেকে ১০০০ পর্যন্ত সঙ্খ্যার গণনার জন্য আমাদের প্রোগ্রাম আগের থেকে বেশ দ্রুত রান হয়েছে। মজার ব্যাপার হচ্ছে এভাবে প্রথম এল্গোরিদমের জন্য সঙ্খ্যা যত বাড়বে গতি তত কমতে থাকবে, অপর দিকে দ্বিতীয় এল্গোরিদমের ক্ষেত্রে সঙ্খ্যা যত বাড়বে গতি আপেক্ষিক ভাবে তত বৃদ্ধি পাবে।
আচ্ছা প্রোগ্রাম ফাস্ট রান হচ্ছে, ক্যাল্কুলেশন ফাস্ট হচ্ছে, কিন্ত আমি এতেও খুশি না। এখানেও সমস্যা আছে। খেয়াল করেদেখুন আমরা এক্সিস্টিং ভ্যালুকে কপি করে এনে একাধিক বার প্রয়োজনীয় স্থানে রাখছি। এতে ক্যাল্কুলেশন টাইম কমছে, কিন্ত মেমোরিতে একই ডাটা বার বার সেভ হচ্ছে। এই অতিরিক্ত ডাটা সেভ হওয়া থেকে আমাদের প্রোগ্রাম কে মুক্ত করতে হবে। কিন্ত কিভাবে?
এই পরিস্থিতিতে সেভিয়ার হিসেবে আগমন ঘটছে আমাদের অন্যতম শক্তিশালি মৌলিক ডাটা স্ট্রাকচার - LinkedList।
Continue...